Veri setindeki herhangi bir değerin kaçıncı yüzdelik dilimde yer aldığını anlamamıza yardımcı olur. Örneğin, 50. persentil, veri setinin tam olarak ortasını ifade eder.
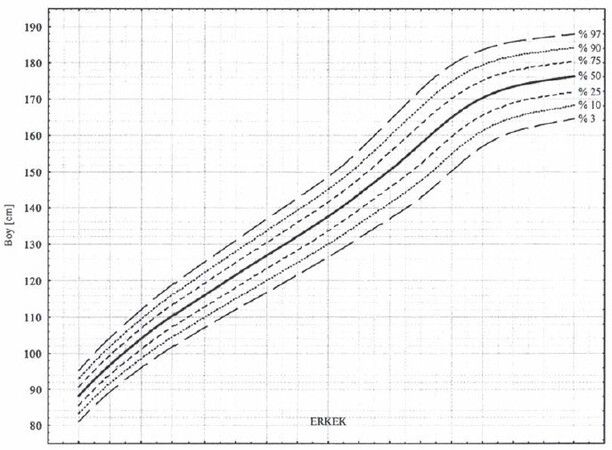
Persentil hesaplamak neden önemlidir?
Persentil hesaplamak, veri setinin dağılımı hakkında bilgi sahibi olmamıza yardımcı olur. Bu sayede, veri setindeki aykırı değerleri belirleme ve genel eğilimleri anlama konusunda bize yol gösterir. Özellikle sağlık sektöründe hasta bilgilerini analiz etmek veya finansal verileri incelemek gibi pek çok alanda persentil hesaplama yöntemleri kullanılır.
Hangi durumlarda persentil hesaplamaları kullanılır?
Persentil hesaplamaları, özellikle büyük veri setlerinin analiz edildiği durumlarda sıklıkla kullanılır. Örneğin, bir okulun sınav sonuçlarını incelemek veya bir şirketin personel performansını değerlendirmek için persentil hesaplama yöntemlerine başvurulabilir. Ayrıca, ürün fiyatlarının belirlenmesi veya pazar araştırmaları gibi alanlarda da persentil hesaplamaları önemli bir rol oynar.
Persentil Hesaplamada Kullanılan Yöntemler
Persentil hesaplamada kullanılan yöntemler arasında en yaygın kullanılanı, verilerin küçükten büyüğe sıralandıktan sonra istenilen persentile denk gelen değerin bulunmasıdır. Bu yöntem, belirli bir veri setinin dağılımını anlamak ve belirli bir yüzde dilimine denk gelen değerleri belirlemek için kullanılır. Bir diğer kullanılan yöntem ise, verilerin sınıflandırılmasından sonra, her sınıfın frekans tablosunun çıkarılmasıdır. Bu frekans tablosu üzerinden, herhangi bir persentilin bulunması ve hesaplanması mümkündür. Ayrıca, persentil hesaplamada kullanılan diğer yöntemler arasında, büyük veri kümeleri için interpolasyon ve extrapolasyon tekniklerinin kullanılması da bulunmaktadır. Bu teknikler, eksik verilerin veya belirli bir aralık dışındaki verilerin persentil hesaplamasında kullanılmasını sağlar.
Örnek Persentil Hesaplama Uygulaması
Örnek Persentil Hesaplama Uygulaması, istatistiksel verilerin dağılımını incelemek ve yorumlamak için sıkça kullanılan bir yöntemdir. Persentil, bir veri setindeki değerlerin yüzdelik dilimlerini ifade eder. Örneğin, 50. persentil medyanı, yani veri setinin orta değerini gösterir. Persentil hesaplama, veri setinin genel dağılımını anlamak ve belirli bir konumda olan değerleri belirlemek için önemli bir araçtır.
Persentil hesaplamada kullanılan yöntemler arasında en yaygın olanı, veri setini sıralayıp istenen yüzdelik dilimi bulmaktır. Örneğin, 75. persentili bulmak için veri setini büyükten küçüğe sıralayıp %75'lik dilimi bulmak gerekmektedir. Bu yöntem, veri setinin içindeki farklı noktalardaki değerleri karşılaştırmak ve yorumlamak için kullanışlı bir araçtır.
Bir örnek persentil hesaplama uygulamasında, elimizde belirli bir veri seti bulunsun. Bu veri setindeki belirli bir persentili hesaplamak istediğimizde, öncelikle veri setini sıralarız. Daha sonra istediğimiz yüzdelik dilimine karşılık gelen değeri buluruz. Bu sayede, veri setindeki değerlerin belirli konumlardaki dağılımını ve eğilimini anlamak mümkün olur.
Persentil hesaplamasının sonuçlarını yorumlarken, veri setinin genel dağılımına ve olayın doğasına dikkat etmek önemlidir. Örneğin, 90. persentilin yüksek olması, veri setindeki değerlerin genellikle yüksek olduğunu gösterebilir. Bu nedenle, persentil hesaplamasının sonuçlarını değerlendirirken, veri setinin genel özelliklerini de göz önünde bulundurmak gerekmektedir.
Persentil Hesaplamasının Sonuçları ve Yorumu
Persentil hesaplaması, istatistiksel verilerin analiz edilmesi ve yorumlanmasında önemli bir rol oynar. Persentil hesaplamasının sonuçları, veri setinin dağılımı hakkında bize değerli bilgiler verir. Örneğin, 25. persentil değeri bize veri setinin en alttaki %25'lik dilimini temsil eder. Bu durumda, verilerin ne kadarının belirli bir değerin altında veya üstünde olduğunu anlamak için persentil hesaplamaları oldukça faydalıdır.
Persentil hesaplamasının sonuçlarına dayanarak, veri setindeki aykırı değerleri tespit etmek de mümkün olabilir. Örneğin, veri setinin 90. persentil değeri bize yüksek değerlerin yer aldığı üst %10'luk dilimi temsil eder. Bu sayede, veri setindeki potansiyel aykırı değerler üzerinde detaylı bir inceleme yapılabilir ve veri setinin güvenilirliği artırılabilir.
Aynı zamanda, persentil hesaplamasının sonuçları veri setinin merkezi eğilimini de belirlemede kullanılabilir. Örneğin, 50. persentil değeri, yani medyan, veri setinin orta noktasını temsil eder. Bu sayede, veri setinin genel dağılımı hakkında daha kapsamlı bir yorum yapılabilir. Dolayısıyla, persentil hesaplamasının sonuçları veri analizinde kritik bir role sahiptir ve doğru yorumlama ile veri setinin anlaşılmasına yardımcı olur.
Persentil hesaplamasının sonuçlarına göre veri setinin dağılımı ve karakteristiği hakkında çeşitli yorumlar yapılabilir. Ancak, bu yorumların doğru ve güvenilir olabilmesi için geniş bir veri seti ve doğru hesaplama metotlarının kullanılması son derece önemlidir. Ayrıca, persentil hesaplamalarının sonuçlarını etkileyebilecek aykırı değerlerin tespit edilmesi ve gerekli düzeltmelerin yapılması da sonuçların daha güvenilir olmasını sağlar.





































